キャリア・エンベロープ・オフセット周波数とパルスの繰り返し周期の制御方法

キャリア・エンベロープ・オフセット周波数f_CEOとパルスの繰り返し周期f_repの制御は、基準信号への位相同期を用いる。基準信号にはマイクロ波周波数基準や光周波数基準を用いる。位相同期は、基準信号と非制御信号の位相差を検出し、その位相差を小さくするように非制御信号発信源、すなわちErモード同期ファイバーレーザーにフィードバック制御を行う。ここでは、f_CEOとf_repの制御について、fixed points理論を用いて論じる。

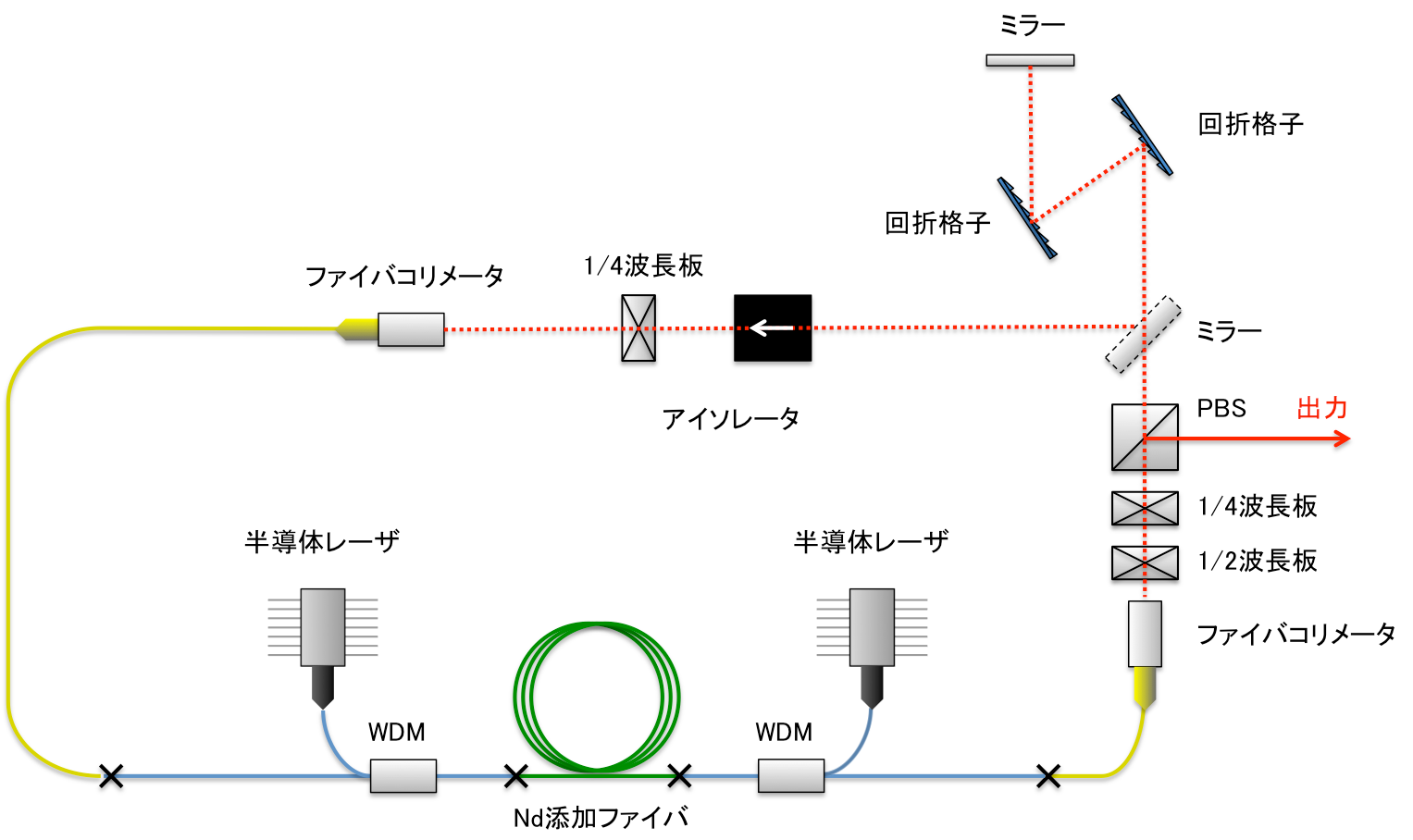
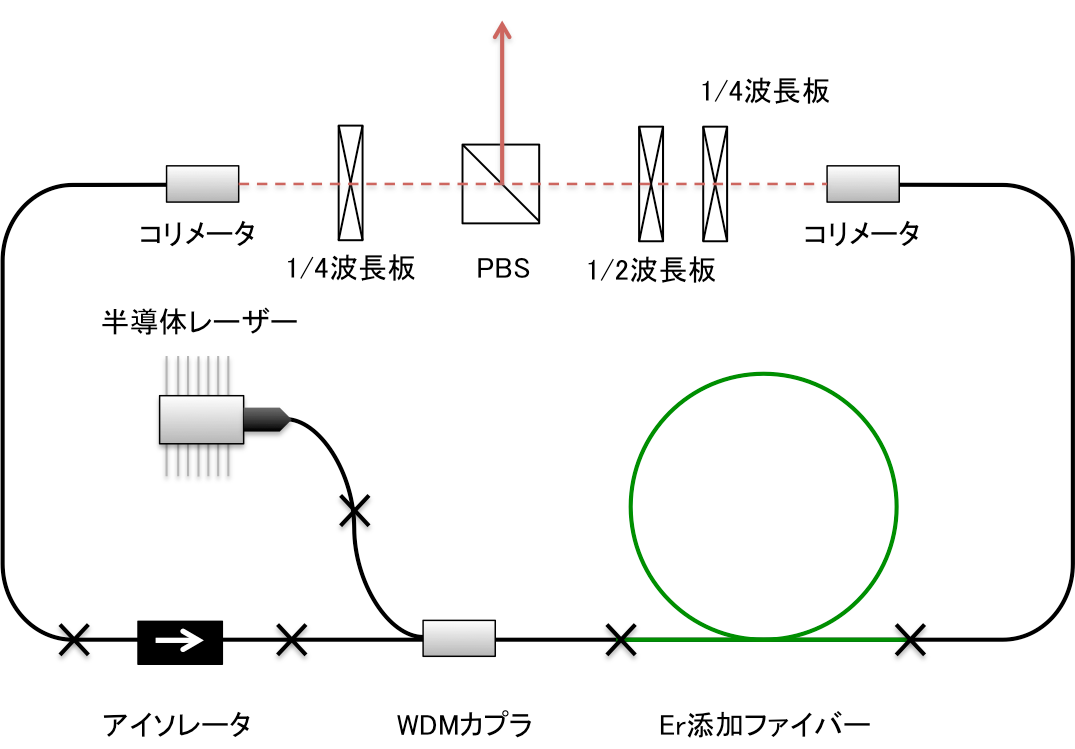
f_CEOの制御法

f_CEOの制御法を論じるために、まずf_CEOの発生原理に立ち戻る。f_CEOはパルス光のキャリアと包絡線の伝搬速度が異なるために、φ_CEPがパルス間で周期的にずれていくために生じている。そこで、群速度と位相速度に変調をかけることができれば、f_CEOの制御ができる。どちらの速度も屈折率に関係している。ファイバーが全てKerr媒質であることから、ファイバー中を伝搬するパルス光には光Kerr効果が生じている。パルス光の強度を変調することは、非線形屈折率n₂を変化させることになり、群速度と位相速度の両方を変化させることができ、f_CEOの制御ができる。パルス光の強度を変調するには、Erモード同期ファイバーレーザーの励起パワーに変調を加えればよい。励起光はLDであり、電流で駆動される。そのため、LD駆動電流にフィードバック制御を行うことで、f_CEOの制御ができると考えられる。

次に、物理的な見地とは別にfixed points理論からf_CEOの制御法を論じる。まず、励起パワーPを変化させたときに、コム全体の揺らぎを考える。すなわち、n番目のコムモードの光周波数をPで微分すればよい。

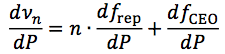
ここで励起パワーの変化に対するfixed pointを考えると、

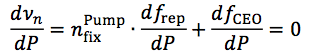
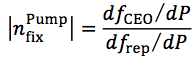
であり、fixed point周波数ν_fix^Pumpは文献[1][2]より

である。これは波長1460 nmあたりを中心にコム全体に変調を与えることができることを意味している。したがって、励起パワーの変化が任意のコムモードに与える周波数変化は

であり、0 Hz付近での変化量が大きい。よって、f_CEOの制御に効果的であるといえる。

f_repの制御法[3]

f_repの制御にはErモード同期ファイバーレーザーの共振器長を制御する。これはレーザーの縦モードの間隔がレーザー共振器長に関係していることから理解できる。f_CEOの制御法と同様に、fixed points理論で論じてみる。

共振器長Lを変化させたときに、コム全体の揺らぎを考えると、

であり、fixed pointは

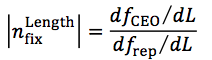
となる。これも実験的に分子分母ともに値を求めることができ、fixed point周波数ν_fix^Lengthは

となる。したがって共振器長を変化させると、光周波数領域のコムモードに大きい周波数変化を与えることができ、fixed points理論が有用であることを示している。

「中嶋善晶, 光周波数標準のためのファイバー型光周波数コム低雑音化に関する研究, 2010.」より。

References and Links

[1] J. J. McFerran, W. C. Swann, B. R. Washburn, and N. R. Newbury, “Elimination of pump-induced frequency jitter on fiber-laser frequency combs,” Opt. Lett. 31, 1997-1999 (2006).
[2] J. J. McFerran, W. C. Swann, B. R. Washburn, and N. R. Newbury, “Suppression of pump-induced frequency noise in fiber-laser frequency combs leading to sub-radian f (ceo) phase excursions,” Applied Physics B-Lasers and Optics 86, 219-227 (2007).
[2] N. R. Newbury and B. R. Washburn, “Low-noise fiber-laser frequency combs,” JOSA B 24, 1756-1770 (2007).