光ソリトン効果 – 生成原理

光ソリトンは、光ファイバーの異常分散領域における分散効果によるパルス広がりと、自己位相変調(SPM)によるパルス圧縮が釣り合ったときに現れる[1-3]。ソリトンという名前は孤立波(Solitary Wave)に由来しており、長距離を伝搬しても波形が崩れず、かつソリトン同士で衝突しても全くその影響を受けない波動のことを指す。光ソリトンは1973年に、米AT＆Tベル研究所の長谷川晃氏により発見された[4]。

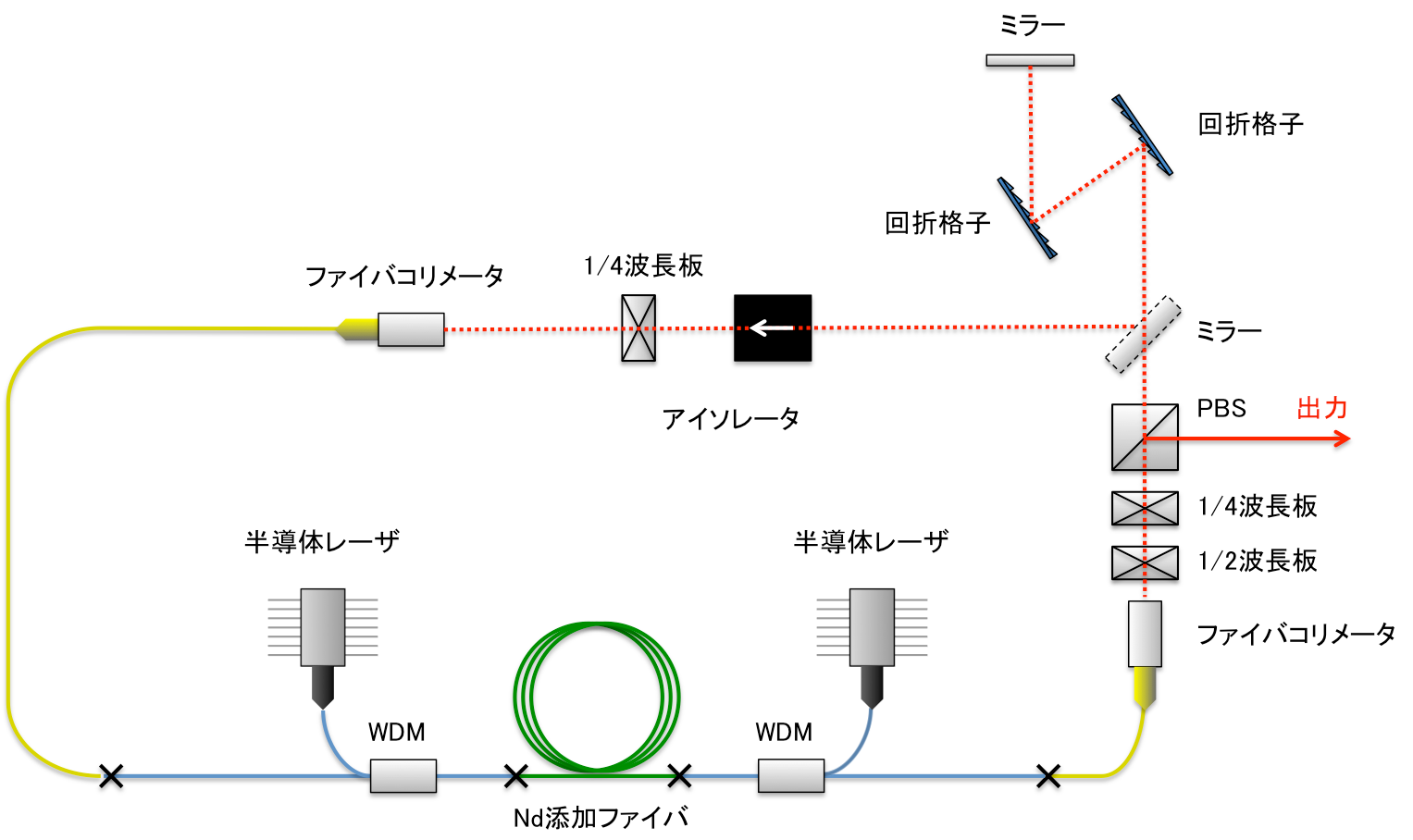
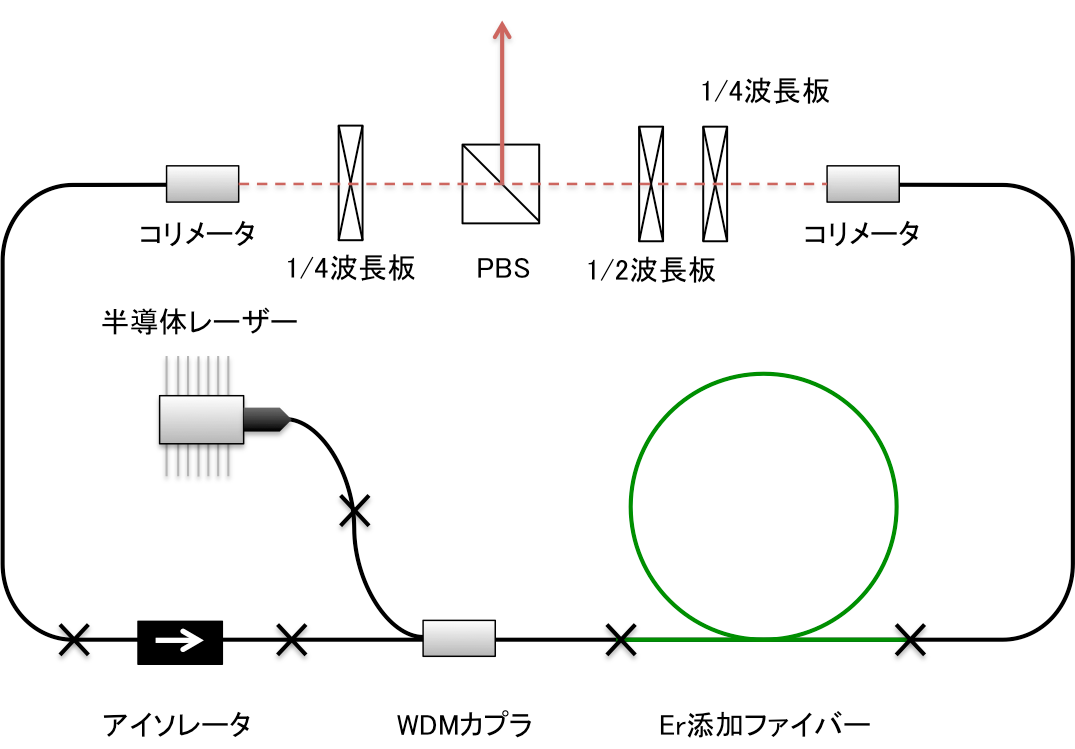
光ファイバーが、入射する光パルスの波長に対し正常分散領域にあるとすると、波長の長い前縁部の成分の伝搬速度は速く、波長の短い後縁部の成分の伝搬速度は遅いためパルスは広がる(波長分散)。さらに正常分散領域ではSPMもパルス広がりに寄与する。

逆に異常分散領域ではパルスの前縁部が遅く、後縁部が速く伝搬する。これにより、異常分散領域では波長分散によってパルス幅が広がる一方で、SPMはパルスを圧縮する方向に働く。このとき、波長分散によるパルス広がりと非線形光学効果による圧縮効果が釣り合うようになると、光ファイバー中の光パルスは波形を保ったまま伝搬するようになる。このときのパルスが光ソリトンであり、このような現象を光ソリトン効果と呼ぶ。図1に光ソリトンの生成原理を示す。

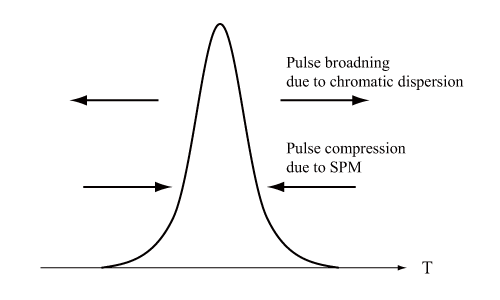
図1：光ソリトンの生成原理

光ソリトンと非線形シュレディンガー方程式

光ソリトンは非線形シュレーディンガー方程式を解くことにより得られる[5]。光パルスの包絡線関数をA(z,T)とすると、光ソリトンは次式のように表される。

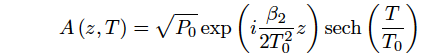光ソリトン …式(1)

ここで、P0は光パルスのピークパワー、T0はパルス幅である。T0は光強度の半値全幅TFWHMとTFWHM=1.763T0の関係にあり、ピークパワーP0は次式を満足しなければならない。

ピークパワー

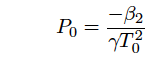
ここで、γは非線形係数である。式(1)を満足するピークパワーより大きなピークパワーをもったパルス入射に対して高次のソリトン解が存在する。このとき、高次ソリトンの次数を決めるソリトン次数Nは

ソリトン次数

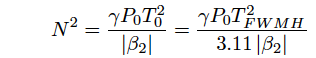
で与えられる。この式からN次のソリトンを生成するには、基本ソリトンの生成時に必要なピークパワーのN2倍のピークパワーが必要であることがわかる。高次ソリトンはそのパルス波形を周期的に変化させながら光ファイバー中を伝搬する。この伝搬の周期はソリトン周期と呼ばれ、次の式で与えられるz0の周期毎にソリトンが形成される。

ソリトン周期

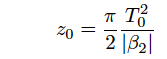
ソリトン次数

ソリトン次数Nはパルスが受ける非線形光学効果と分散効果のうち、どちらが支配的かを表すパラメータであるといえる。

N<1の場合

N<1の場合　(厳密には入射時にソリトン次数が0.5よりも小さい場合のみこの条件に当てはまる)、分散の影響が強いため、パルスは光ソリトンを形成することなく、伝搬とともにパルス幅は広がっていく。

N=1の場合

分散と非線形光学効果の影響力は拮抗しており、そのために1次のソリトンパルスは時間的にも、スペクトル的にも同じ波形を保ったまま光ファイバー中を伝搬し、基本ソリトンと呼ばれる。

N>1の場合

N>1の高次ソリトンは、光ファイバー中を一定の周期で波形を変えながら伝搬することが知られている。高次ソリトンにおいて特に注目すべきは、周期のはじめに必ずパルス圧縮の過程が生じることである。これは初期の段階で非線形光学効果の影響が強いために、SPMによるチャープが引き起こすパルス圧縮が分散によるパルス広がりよりも急激に起こるためである。この過程は高次ソリトン圧縮と呼ばれ、超短パルス生成に利用される。高次ソリトン圧縮は、ソリトン次数Nに依存した比率だけパルスを圧縮し、先ほど述べた正常分散ファイバーと異常分散媒質を用いたパルス圧縮よりもかなり大きな圧縮因子を得ることができる。しかし、高次ソリトン圧縮ではパルスの中央成分のみ圧縮され、両翼の成分が圧縮されずに台座のような形で現れる。

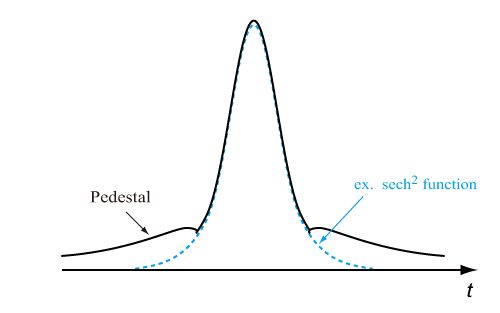
図2：ペデスタルの概念図

この台座の成分はペデスタル(pedestal)といい、パルスの裾の部分で、ある関数形(例:sech型関数)に一致せず、時間遅延に対して減衰すべき関数値よりも大きな成分を指す(図2)。これはSPMで誘起されるチャープはパルスの中心部分でのみ直線的であり、中心部分のみがファイバーの異常分散により圧縮されるために起こる。ペデスタルはソリトン次数Nが大きくなるほど大きくなる。